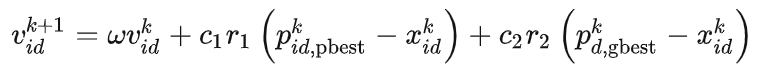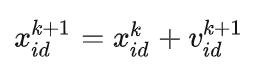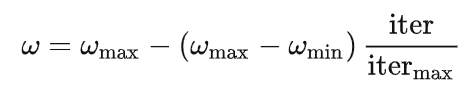算法学习基础-粒子群算法

背景知识

1995年，受到鸟群觅食行为的规律性启发，James Kennedy和Russell Eberhart建立了一个简化算法模型，经过多年改进最终形成了粒子群优化算法(Particle Swarm Optimization, PSO) ，也可称为粒子群算法。

特点

粒子群算法具有收敛速度快、参数少、算法简单易实现的优点（对高维度优化问题，比遗传算法更快收敛于最优解），但是也会存在陷入局部最优解的问题

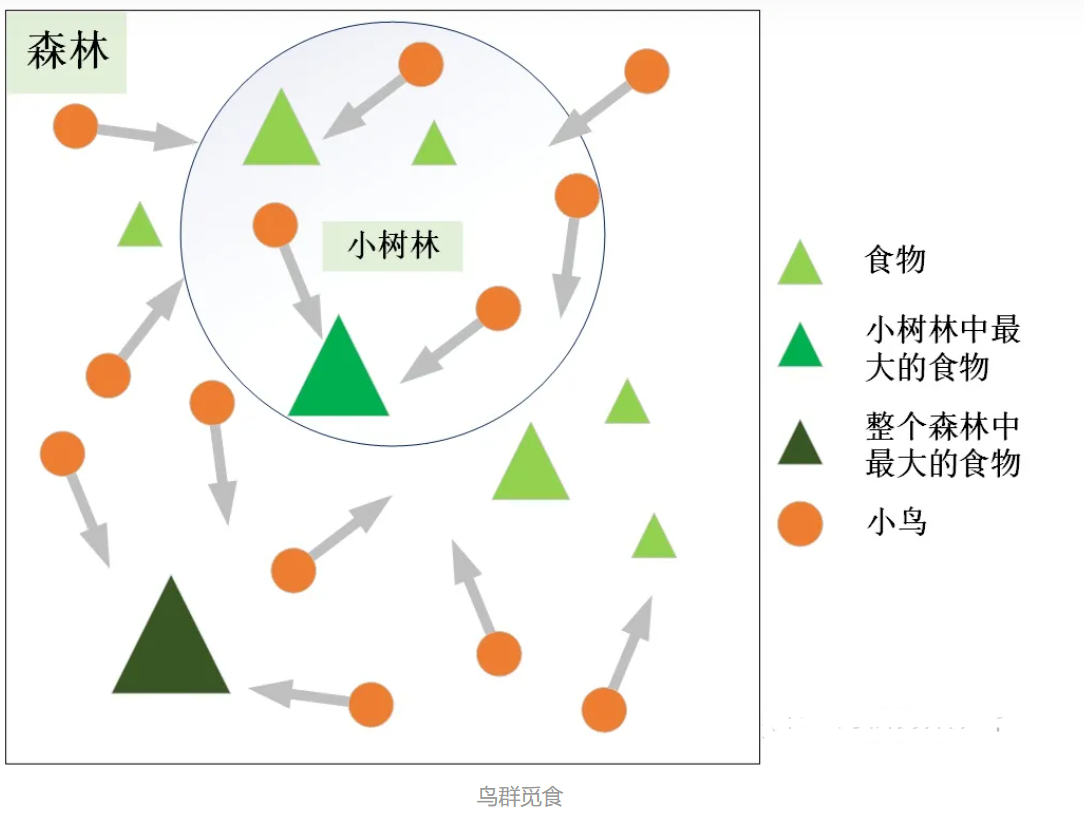
基本思想

粒子群算法的思想源于对鸟群觅食行为的研究，鸟群通过集体的信息共享使群体找到最优的目的地。如下图，设想这样一个场景：鸟群在森林中随机搜索食物，它们想要找到食物量最多的位置。但是所有的鸟都不知道食物具体在哪个位置，只能感受到食物大概在哪个方向。每只鸟沿着自己判定的方向进行搜索，并在搜索的过程中记录自己曾经找到过食物且量最多的位置*，同时所有的鸟都共享自己每一次发现食物的位置以及食物的量，这样鸟群就知道当前在哪个位置食物的量最多。在搜索的过程中每只鸟都会根据自己记忆中食物量最多的位置和当前鸟群记录的食物量最多的位置调整自己接下来搜索的方向。鸟群经过一段时间的搜索后就可以找到森林中哪个位置的食物量最多（全局最优解）。

鸟群觅食.png

算法的基本原理

将鸟群觅食行为和算法原理对应，如下图：

鸟群觅食	粒子群算法
鸟	粒子
森林	求解空间
食物的量	目标函数值（适应值）
每只鸟所处的位置	空间中的一个解（粒子位置）
食物量最多的地方	全局最优解

PSO的基础：信息的社会共享
粒子的两个属性：速度和位置（算法的两个核心要素）

速度表示粒子下一步迭代时移动的方向和距离，位置是所求解问题的一个解。
算法的6个重要参数

假设在 D 维搜索空间中，有 N 个粒子，每个粒子代表一个解，则：
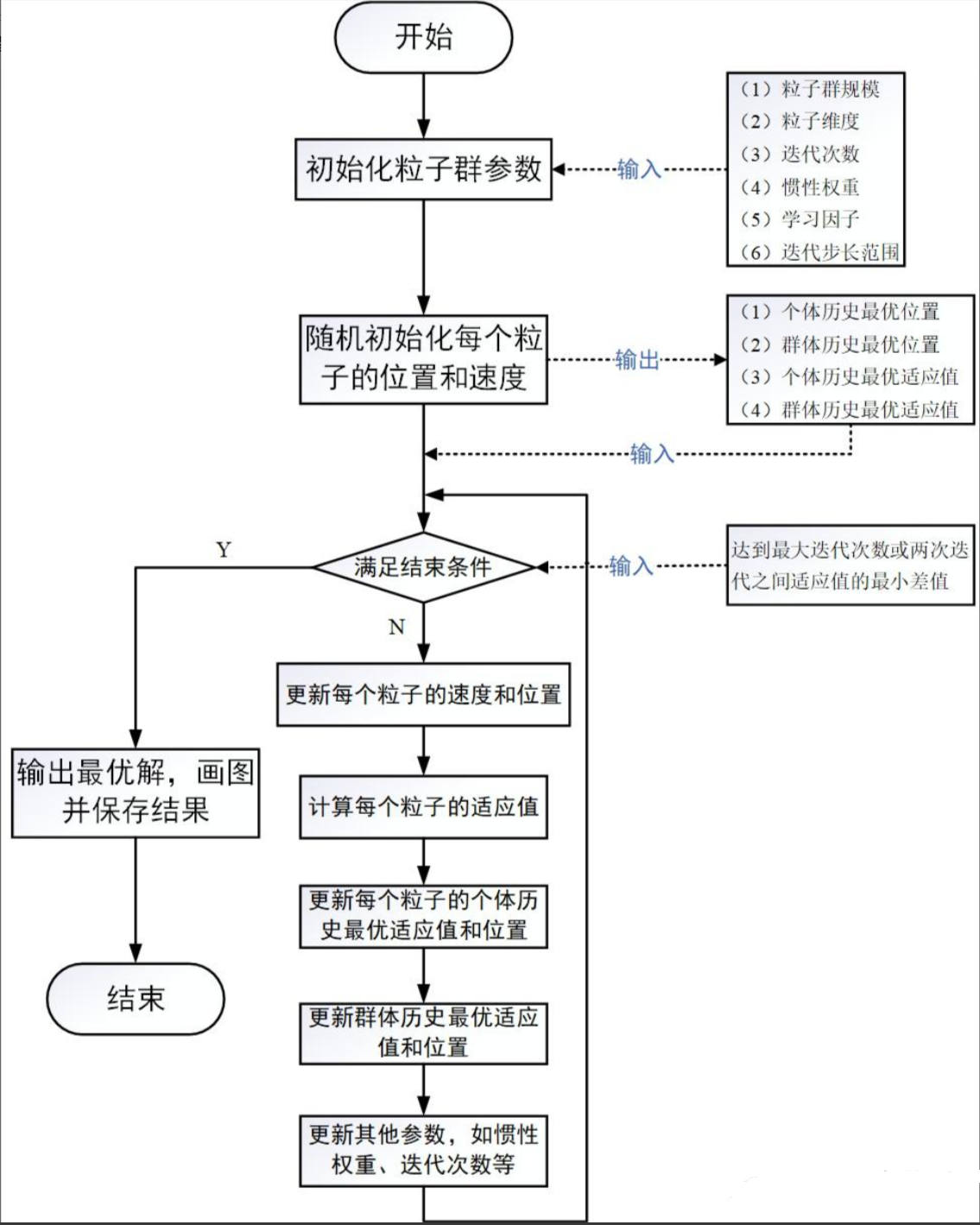
粒子群算法的流程图
伪代码

速度更新公式

表述上叫速度，实际上就是粒子下一步迭代移动的距离和方向，也就是一个位置向量。
速度更新公式.png

速度更新公式的解释

① 第一项：惯性部分

由惯性权重和粒子自身速度构成，表示粒子对先前自身运动状态的信任。

② 第二项：认知部分

表示粒子本身的思考，即粒子自己经验的部分，可理解为粒子当前位置与自身历史最优位置之间的距离和方向。

③ 第三项：社会部分

表示粒子之间的信息共享与合作，即来源于群体中其他优秀粒子的经验，可理解为粒子当前位置与群体历史最优位置之间的距离和方向。

速度更新公式的参数定义

参数定义.png

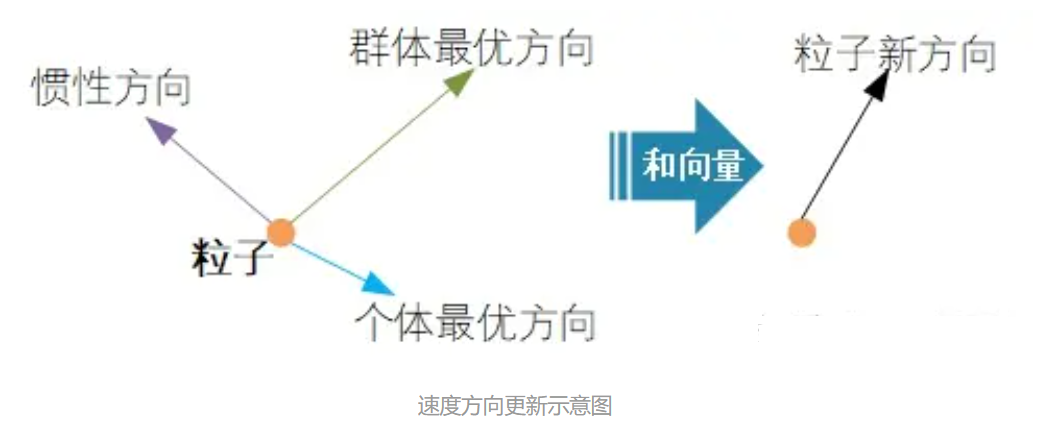
速度的方向

粒子下一步迭代的移动方向 = 惯性方向 + 个体最优方向 + 群体最优方向
速度方向.png

位置更新公式

上一步的位置 + 下一步的速度
位置更新公式.png

算法参数解释

粒子群规模 N ：

一个正整数，推荐取值范围：[20,1000]，简单问题一般取20~40，较难或特定类别的问题可以取100~200。较小的种群规模容易陷入局部最优；较大的种群规模可以提高收敛性，更快找到全局最优解，但是相应地每次迭代的计算量也会增大；当种群规模增大至一定水平时，再增大将不再有显著的作用。
粒子维度 D :

粒子搜索的空间维数即为自变量的个数。
迭代次数 K ：
推荐取值范围：[50,100]，典型取值：60、70、100；这需要在优化的过程中根据实际情况进行调整，迭代次数太小的话解不稳定，太大的话非常耗时，没有必要。
惯性权重 w ：

动态调整惯性权重以平衡收敛的全局性和收敛速度,惯性权重 w 表示上一代粒子的速度对当代粒子的速度的影响，或者说粒子对当前自身运动状态的信任程度，粒子依据自身的速度进行惯性运动。惯性权重使粒子保持运动的惯性和搜索扩展空间的趋势。 w 值越大，探索新区域的能力越强，全局寻优能力越强，但是局部寻优能力越弱。反之，全局寻优能力越弱，局部寻优能力强。较大的 w 有利于全局搜索，跳出局部极值，不至于陷入局部最优；而较小的 w 有利于局部搜索，让算法快速收敛到最优解。当问题空间较大时，为了在搜索速度和搜索精度之间达到平衡，通常做法是使算法在前期有较高的全局搜索能力以得到合适的种子，而在后期有较高的局部搜索能力以提高收敛精度，所以 w 不宜为一个固定的常数.

当 w = 1 时，退化成基本粒子群算法，当 w = 0 时，失去对粒子本身经验的思考。推荐取值范围：[0.4,2]，典型取值：0.9、1.2、1.5、1.8
- 改善惯性权重 w:
在解决实际优化问题时，往往希望先采用全局搜索，使搜索空间快速收敛于某一区域，然后采用局部精细搜索以获得高精度的解。因此提出了自适应调整的策略，即随着迭代的进行，线性地减小 w 的值。这里提供一个简单常用的方法——线性变化策略：随着迭代次数的增加，惯性权重 w 不断减小，从而使得粒子群算法在初期具有较强的全局收敛能力，在后期具有较强的局部收敛能力。
学习因子 c1和c2
也称为加速系数或加速因子（这两个称呼更加形象地表达了这两个系数的作用）
- c1 表示粒子下一步动作来源于自身经验部分所占的权重，将粒子推向个体最优位置
  的加速权重；
- c2 表示粒子下一步动作来源于其它粒子经验部分所占的权重，将粒子推向群体最优位置
  的加速权重；
- c1=0：无私型粒子群算法，”只有社会，没有自我”，迅速丧失群体多样性，易陷入局部最优而无法跳出；
- c2=0：自我认知型粒子群算法，”只有自我，没有社会”，完全没有信息的社会共享，导致算法收敛速度缓慢；
- c1,c2都不为0：完全型粒子群算法，更容易保持收敛速度和搜索效果的均衡，是较好的选择。
  
  低的值使粒子在目标区域外徘徊，而高的值导致粒子越过目标区域。推荐取值范围：[0,4]；典型取值： c1=c2=2、c1=1.6和c2=1.8 、 c1=1.6和c2=2 ，针对不同的问题有不同的取值，一般通过在一个区间内试凑来调整这两个值。

算法中的重要概念

适应值（fitness values）

即优化目标函数的值，用来评价粒子位置的好坏程度，决定是否更新粒子个体的历史最优位置和群体的历史最优位置，保证粒子朝着最优解的方向搜索。
位置限制
限制粒子搜索的空间，即自变量的取值范围，对于无约束问题此处可以省略。
速度限制

为了平衡算法的探索能力与开发能力，需要设定一个合理的速度范围，限制粒子的最大速度 v_max，即粒子下一步迭代可以移动的最大距离。
- v_max较大时，粒子飞行速度快，探索能力强，但粒子容易飞过最优解；
- v_max较小时，飞行速度慢，开发能力强，但是收敛速度慢，且容易陷入局部最优解；
- v_max一般设为粒子变化范围的10％~20％，可根据实际情况调试，但不能大于粒子(解)的变化范围。
优化停止准则

① 最大迭代步数

② 可接受的满意解：上一次迭代后最优解的适应值与本次迭代后最优解的适应值之差小于某个值后停止优化
初始化

需要根据具体的问题进行分析，如果根据我们的经验判断出最优解一定在某个范围内，则就在这个范围内初始化粒子。如果无法确定，则以粒子的取值边界作为初始化范围。

算法实现

使用粒子群算法优化Rosenbrock函数。
Rosenbrock函数的数学表示通常为
Rosenbrock函数是一个非凸函数，通常用于测试优化算法的性能。
找到Rosenbrock函数的最小值

x_i∈[-30,30]（i=1,2,3,4）,最大速度Vmax = 60，粒子数量为5，维度为6

解：全局最小值仍然位于一个 n-维数组中的所有元素都等于1的点，此时函数值为0

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def fit_fun(x):  # 适应函数
    return sum(100.0 * (x[0][1:] - x[0][:-1] ** 2.0) ** 2.0 + (1 - x[0][:-1]) ** 2.0)


class Particle:
    # 初始化
    def __init__(self, x_max, max_vel, dim):
        self.__pos = np.random.uniform(-x_max, x_max, (1, dim))  # 粒子的位置
        self.__vel = np.random.uniform(-max_vel, max_vel, (1, dim))  # 粒子的速度
        self.__bestPos = np.zeros((1, dim))  # 粒子最好的位置
        self.__fitnessValue = fit_fun(self.__pos)  # 适应度函数值

    def set_pos(self, value):
        self.__pos = value

    def get_pos(self):
        return self.__pos

    def set_best_pos(self, value):
        self.__bestPos = value

    def get_best_pos(self):
        return self.__bestPos

    def set_vel(self, value):
        self.__vel = value

    def get_vel(self):
        return self.__vel

    def set_fitness_value(self, value):
        self.__fitnessValue = value

    def get_fitness_value(self):
        return self.__fitnessValue


class PSO:
    # 4, 5, 10000, 30, 60, 1e-4, C1=2, C2=2, W=1
    def __init__(self, dim, size, iter_num, x_max, max_vel, tol, best_fitness_value=float('Inf'), C1=2, C2=2, W=1):
        self.C1 = C1
        self.C2 = C2
        self.W_max = W
        self.W_min = 0.5
        self.W = W
        self.dim = dim  # 粒子的维度
        self.size = size  # 粒子个数
        self.iter_num = iter_num  # 迭代次数
        self.x_max = x_max  # 位置取值范围
        self.max_vel = max_vel  # 粒子最大速度
        self.tol = tol  # 截至条件
        self.best_fitness_value = best_fitness_value
        self.best_position = np.zeros((1, dim))  # 种群最优位置
        self.fitness_val_list = []  # 每次迭代最优适应值

        # 对种群进行初始化
        self.Particle_list = [Particle(self.x_max, self.max_vel, self.dim) for i in range(self.size)]

    def set_bestFitnessValue(self, value):
        self.best_fitness_value = value

    def get_bestFitnessValue(self):
        return self.best_fitness_value

    def set_bestPosition(self, value):
        self.best_position = value

    def get_bestPosition(self):
        return self.best_position

    # 更新速度
    def update_vel(self, part):
        vel_value = self.W * part.get_vel() + self.C1 * np.random.rand() * (part.get_best_pos() - part.get_pos()) \
                    + self.C2 * np.random.rand() * (self.get_bestPosition() - part.get_pos())
        # 超过速度最大值和最小值就将值设为最大会最小值
        vel_value[vel_value > self.max_vel] = self.max_vel
        vel_value[vel_value < -self.max_vel] = -self.max_vel
        part.set_vel(vel_value)

    # 更新位置
    def update_pos(self, part):
        pos_value = part.get_pos() + part.get_vel()
        part.set_pos(pos_value)
        value = fit_fun(part.get_pos())
        if value < part.get_fitness_value():
            part.set_fitness_value(value)
            part.set_best_pos(pos_value)
        if value < self.get_bestFitnessValue():
            self.set_bestFitnessValue(value)
            self.set_bestPosition(pos_value)

    def update_ndim(self):

        for i in range(self.iter_num):
            self.W = self.W_max - (self.W_max - self.W_min) * i / self.iter_num # 可以去掉这样权重就是一个固定不变的值
            for part in self.Particle_list:
                self.update_vel(part)  # 更新速度
                self.update_pos(part)  # 更新位置
            self.fitness_val_list.append(self.get_bestFitnessValue())  # 每次迭代完把当前的最优适应度存到列表
            print('第{}次最佳适应值为{}'.format(i, self.get_bestFitnessValue()))
            if self.get_bestFitnessValue() < self.tol:
                break

        return self.fitness_val_list, self.get_bestPosition()

if __name__ == '__main__':
    # test 香蕉函数
    pso = PSO(4, 5, 10000, 30, 60, 1e-4, C1=2, C2=2, W=1.2)
    fit_var_list, best_pos = pso.update_ndim()
    print("最优位置:" + str(best_pos))
    print("最优解:" + str(fit_var_list[-1]))
    plt.plot(range(len(fit_var_list)), fit_var_list, alpha=0.5)