算法学习基础-P、NP问题
P问题:
如果一个问题可以在多项式时间内解决,即问题的输入规模n的某个固定次方的时间内解决,那么这个问题就被称为P问题。例如,排序问题和查找问题都是P问题,有多项式时间算法,算得很快的问题。。
NP问题:
如果一个问题可以在多项式时间内验证其解的正确性,那么这个问题就被称为NP问题。算起来不确定快不快的问题,但是我们可以快速验证这个问题的解。
NP-complete问题:
属于NP问题,且属于NP-hard问题。
NP-hard问题:
比NP问题都要难的问题。
理解
- 多项式: axn+bxn-1+c ,形如这种形式的就被称为x的最高位为n的多项式。
- 时间复杂度:它可以用来表示一个算法运行的时间效率。举个例子,冒泡排序的时间复杂度为O(n2),取其最高次,可以看出,这是一个时间复杂度为多项式的表示方式。
在排序这个大问题里,是可以找到一种时间复杂度为O(n2)多项式的算法(如冒泡排序法)来求解排序问题的,所以我们说排序问题是一个有多项式时间算法的问题,即属于P类问题。
P问题:
存在多项式时间算法的问题。(P:polynominal,多项式)。
我们为什么要研究这个P类问题呢?当计算机处理的数据达到100万个的时候,时间复杂度分别为 O(n2)和O(en)的算法,运行时间简直就是天壤之别。所以我们才要研究一个问题是否具有多项式时间的算法。
NP问题
能在多项式时间内验证得出一个正确解的问题。(NP:Nondeterministic polynominal,非确定性多项式)。
这里可以清楚的看出P类问题是NP类问题的子集(即存在多项式时间算法的问题,总能在多项式时间内验证它)
这里的“非确定性”指的是在验证解的正确性时,可以使用一些猜测或者非确定性的方法,或者是指不知道这个问题存不存在一个多项式时间的算法(可能只是不知道,不是不存在)。例如,旅行商问题和图的着色问题都是NP问题
是否 NP类问题=P类问题?
即,是否所有能在多项式时间内验证得出正确解的问题,都是具有多项式时间算法的问题呢?
要是解决了这个问题,那岂不是所有的NP问题都可以通过计算机来解决?
为了证明这个千古难题,科学家想出了很多办法。其中之一就是问题的约化。所谓问题约化就是,可以用问题B的算法来解决A ,我们就说问题A可以约化成问题B。举个例子:一元一次方程的求解,跟二元一次方程的求解,我们知道,只要能求解二元一次方程,那就可以用二元一次方程的解法来求解一元一次方程,只需要将一元一次方程加上y,并附加一个方程y=0就可以将一元一次方程变形为一个二元一次方程,然后用二元一次方程的解法来求解这个方程。注意,这里二元一次方程的解法会比一元一次的复杂。所以我们说,只需要找到解二元一次方程的规则性解法,那就能用这个规则性解法来求解一元一次方程。从这里也可以看出,约化是具有传递性的,如A约化到B,B约化到C,A就可以约化到C,同时不断约化下去,我们会发现一个很惊人的特性,就是他一定会存在一个最大的问题,而我们只需要解决了这个问题,那其下的所有问题也就解决啦!这就是我们所说的NPC问题的概念!!!
引到NP问题里就是,对于同一类的所有的NP类问题,若他们都可以在多项式时间内约化成最难的一个NP类问题,(我们直观的认为,被约化成的问题应具有比前一个问题更复杂的时间复杂度)当我们针对这个时间复杂度最高的超级NP问题要是能找到他的多项式时间算法的话,那就等于变向的证明了其下的所有问题都是存在多项式算法的,即NP=P!!!!给出NPC问题定义。
NPC类问题(Nondeterminism Polynomial complete):
存在这样一个NP问题,所有的NP问题都可以约化成它(更复杂)。换句话说,只要解决了这个问题,那么所有的NP问题都解决了。其定义要满足2个条件:
- 首先,它得是一个NP问题;
- 所有的NP问题都可以约化到它。
NP难问题(NP-hard问题):
NP-Hard,它满足NPC问题定义的第二条但不一定要满足第一条(就是说,NP-Hard问题要比 NPC问题的范围广,NP-Hard问题没有限定属于NP),即所有的NP问题都能约化到它,但是它不一定是一个NP问题。
NP-Hard问题同样难以找到多项式的算法,但它不列入我们的研究范围,因为它不一定是NP问题。即使NPC问题发现了多项式级的算法,NP-Hard问题有可能仍然无法得到多项式级的算法。事实上,由于NP-Hard放宽了限定条件,它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。
以上四个问题他们之间的关系可以用下图来表示: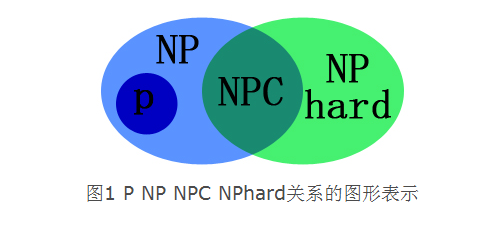
典型示例:
P问题:排序问题、查找问题。
NP问题:旅行商问题、图的着色问题、背包问题。
NP-complete问题:图的着色问题、哈密尔顿回路问题、3-SAT问题。
NP-hard问题:图的同构问题、子集和问题、0-1背包问题。





