二分图

定义

二分图是图论中的一种特殊模型。若能将无向图G=(V,E)的顶点V划分为两个交集为空的顶点集，并且任意边的两个端点都分属于两个集合，则称图G为一个为二分图。

二分图（Bipartite graph）是一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连。下图是典型的二分图。

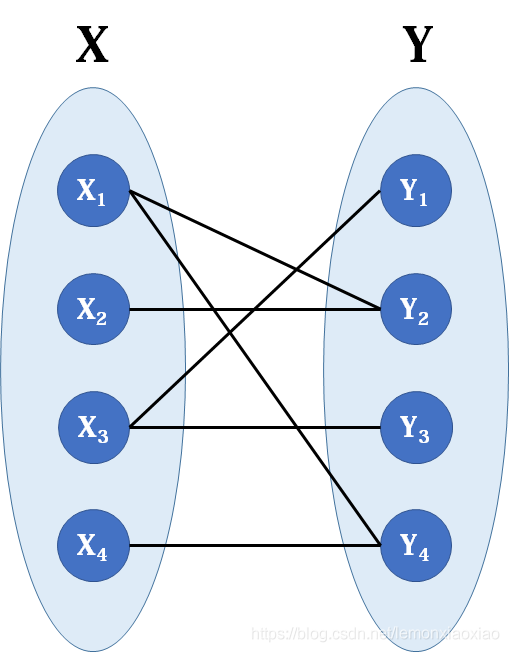
二分图example.png

匹配

图G的一个匹配是由一组没有公共端点的不是圈的边构成的集合。

匹配exmaple.png

匹配的两个重点：1. 匹配是边的集合；2. 在该集合中，任意两条边不能有共同的顶点。

  • 最大匹配

选择这样的边数最大的子集称为图的最大匹配问题。最大匹配的边数称为最大匹配。

  • 完美匹配

如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完美匹配（完全匹配），也称作完备匹配。

考虑部集为X={x1 ,x2, …}和Y={y1, y2, …}的二分图，一个完美匹配就是定义从X-Y的一个双射，依次为x1, x2, … xn找到配对的顶点，最后能够得到 n！个完美匹配。

  • 最优匹配

最优匹配又称为带权最大匹配，是指在带有权值边的二分图中，求一个匹配使得匹配边上的权值和最大。

一般X和Y集合顶点个数相同，最优匹配也是一个完备匹配，即每个顶点都被匹配。如果个数不相等，可以通过补点加0边实现转化。一般使用KM算法解决该问题。

  • 最小覆盖

二分图的最小覆盖分为最小顶点覆盖和最小路径覆盖：

  1. 最小顶点覆盖是指最少的顶点数使得二分图G中的每条边都至少与其中一个点相关联，二分图的最小顶点覆盖数=二分图的最大匹配数；（最小顶点覆盖数 = 3（参照二分图定义中的图））倒过来说就是，删除包含这些点的边，可以删掉所有边。
  2. 最小路径覆盖也称为最小边覆盖，是指用尽量少的不相交简单路径覆盖二分图中的所有顶点。二分图的最小路径覆盖数=|V|-二分图的最大匹配数；（最小边覆盖=8-3=5）
  • 最大独立集

最大独立集是指寻找一个点集，使得其中任意两点在图中无对应边。对于一般图来说，最大独立集是一个NP完全问题，对于二分图来说：最大独立集=|V|-二分图的最大匹配数。

  • 交替路

从未匹配点出发，依次经过未匹配的边和已匹配的边，最终到达另一个未匹配的顶点的路径，即为交替路，如Fig.3：3 -> 5 -> 1 -> 7 -> 4 -> 8（图中红色的就是已匹配的边）

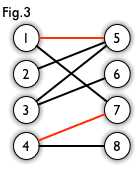
交替路.jpg

  • 增广路（也称增广轨或交错轨）

如果交替路经过除出发点外的另一个未匹配点，则这条交替路称为增广路，如交替路概念的例子，其途径点8，即为增广路。

由增广路的定义推出下面三个结论（设P为一条增广路）：

1). P的路径长度一定为奇数，第一条边和最后一条边都是未匹配的边（根据要途经已匹配的边和要经过另一个未匹配点，这个结论可以理解成第一个点和最后一个点都是未匹配点，可以在Fig.3上的增广路观察到）

2).对增广路径编号，所有奇数的边都不在M中，偶数边在M中。

3). P经过取反操作可以得到一个更大的匹配图，比原来匹配多一个（取反操作即，未匹配的边变成匹配的边，匹配的边变成未匹配的边，这个结论根据结论1).和交替路概念可得该结论）

4). 当且仅当不存在关于图M的增广路径，则图M为最大匹配。所以匈牙利算法的思路就是：不停找增广路，并增加匹配的个数。

匈牙利算法

匈牙利算法主要用来解决两个问题：求二分图的最大匹配数和最小点覆盖数。

匈牙利算法的核心就是寻找增广路。具体而言，匈牙利算法从二分图中没有匹配的点开始寻找增广路径。找到增广路后，根据增广路径的性质，显然路径里没被匹配的连线比已经匹配了的连线多一条，于是对增广路径中的边进行取反操作，这样匹配数就比原来多1个。不断执行上述操作，直到找不到增广路径为止，无法找到增广路径说明已达到最大匹配。

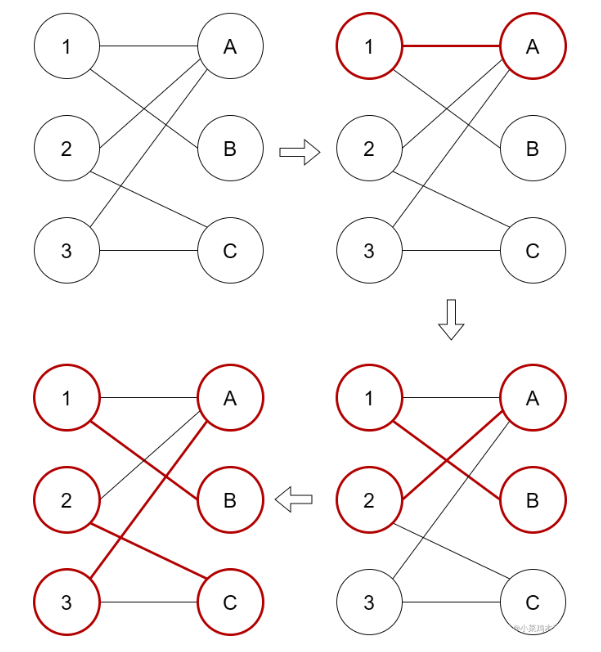
匈牙利算法example.png

  1. 首先从未匹配点1开始寻找增广路，找到了另一个未匹配点A说明找到了增广路，停止寻找，进行取反操作，将非匹配边变为匹配边，于是1-A为匹配边。
  2. 从未匹配点2开始寻找增广路，显然2->A->1->B为增广路，进行取反，于是此时匹配边为2-A、1-B。
  3. 从未匹配点3开始寻找增广路，显然3->A->2->C为增广路，进行取反，于是匹配边变为3-A、2-C、1-B。因为已经不存在未匹配点，此时已经找不到更多增广路径，因此达到了此二分图的最大匹配。

注：显然，二分图匹配结果并不唯一。

另一种想法，但是代码实现是一样的

最大匹配问题相当于，假如你是红娘，可以撮合任何一对有暧昧关系的男女，那么你最多能成全多少对情侣？（数学表述：在二分图中最多能找到多少条没有公共端点的边）

我们从B1看起（男女平等，从女生这边看起也是可以的），他与G2有暧昧，那我们就先暂时把他与G2连接（注意这时只是你作为一个红娘在纸上构想，你没有真正行动，此时的安排都是暂时的）。

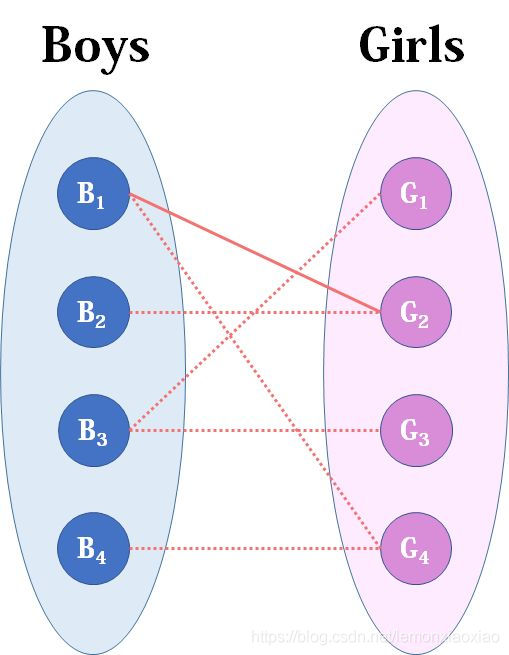
p1.png

来看B2，B2也喜欢G2，这时G2已经“名花有主”了（虽然只是我们设想的），那怎么办呢？我们倒回去看G2目前被安排的男友，是B1，B1有没有别的选项呢？有，G4，G4还没有被安排，那我们就给B1安排上G4。

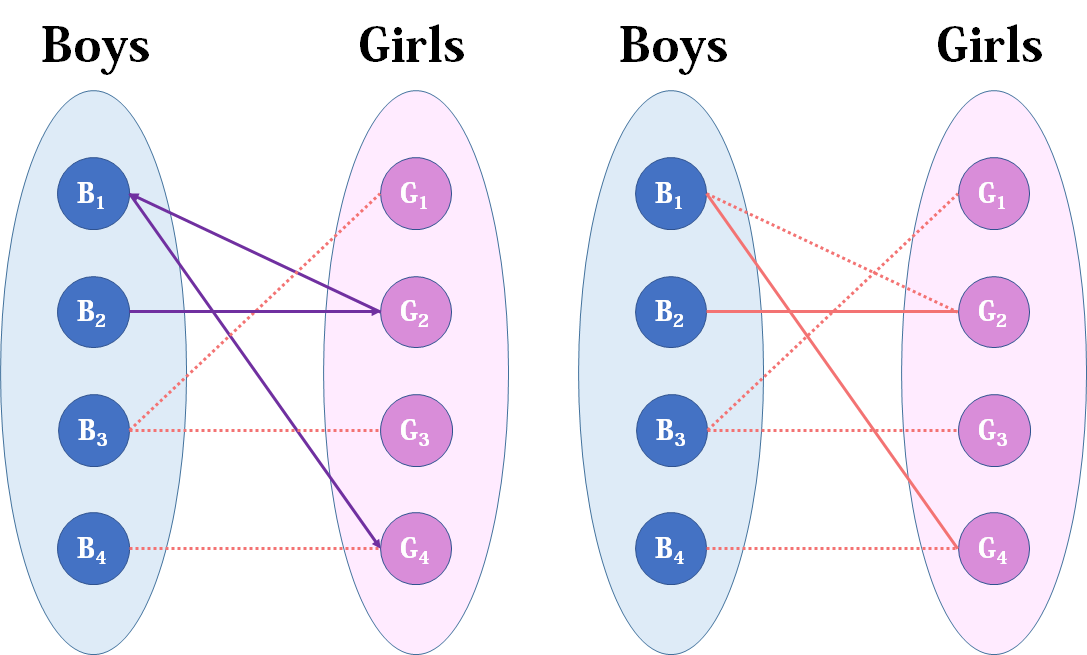
p2.png

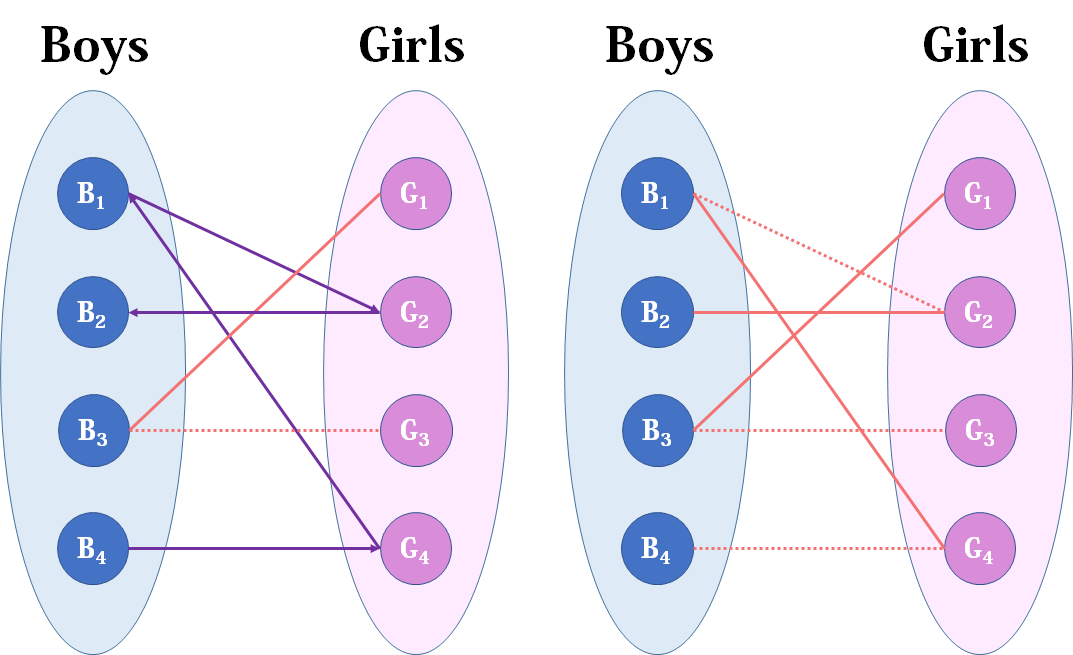
然后B3，B3直接配上G1就好了，这没什么问题。至于B4，他只钟情于G4，G4目前配的是B1。B1除了G4还可以选G2，但是呢，如果B1选了G2，G2的原配B2就没得选了。我们绕了一大圈，发现B4只能注定单身了，可怜。（其实从来没被考虑过的G3更可怜）

p3.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
const int MAXM = 50;
const int MAXN = 50;

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过

// 该函数试图找到从给定左侧节点开始的增广路径,但不是找完整条路径在翻转的，而是有未匹配的边就翻转。
bool match(int i)
{
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]) //有边且未访问
        {
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}

int Hungarian()
{
    int cnt = 0;
    for (int i = 1; i <= M; ++i)
    {
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}


int main()
{
    M = 3, N = 3;
    memset(Map, 0, sizeof(Map));
    memset(p, 0, sizeof(p));
    Map[1][1] = 1;
    Map[1][2] = 1;
    Map[2][1] = 1;
    Map[2][3] = 1;
    Map[3][1] = 1;
    Map[3][3] = 1;
    cout << Hungarian();

    M = 4, N = 4;
    memset(Map, 0, sizeof(Map));
    memset(p, 0, sizeof(p));
    Map[1][2] = 1;
    Map[1][4] = 1;
    Map[2][2] = 1;
    Map[3][1] = 1;
    Map[3][3] = 1;
    Map[4][4] = 1;
    cout << Hungarian();
}

使用了一个递归的技巧，我们不断往下递归，尝试寻找合适的匹配。

KM算法

KM算法（Kuhn－Munkres），用来求带权二分图的最大权匹配（最优匹配）。

问题引出

如果一个公司里每个员工做每件工作的效率各不相同，我们如何得到一个最优匹配使得整个公司的工作效率最大呢？

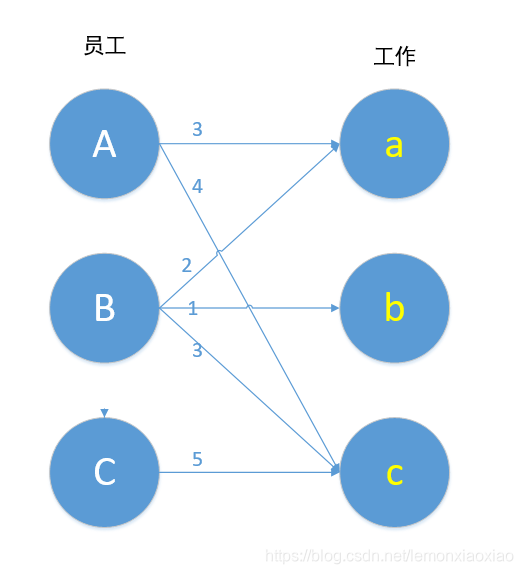
question.png

不了解KM算法的人如何解决这个问题？我们只需要用匈牙利算法找到所有的最大匹配，比较每个最大匹配的权重，再选出最大权重的最优匹配即可。这不失为一个解决方案，但是，如果公司员工的数量越来越多，此种算法的实行难度也就越来越大，我们必须另辟蹊径：KM算法。

数学表示形式为

KM算法数学表述.png

算法步骤

首先对每个顶点赋值，将左边的顶点赋值为最大权重，右边的顶点赋值为0。

m1.png

进行匹配，我们匹配的原则是：只与权重相同的边匹配，若是找不到边匹配，对此条路径的所有左边顶点-1，右边顶点+1，再进行匹配，若还是匹配不到，重复+1和-1操作。（这里看不懂可以跳过，直接看下面的操作，之后再回头来看这里。）

对A进行匹配，符合匹配条件的边只有Ac边。匹配成功！

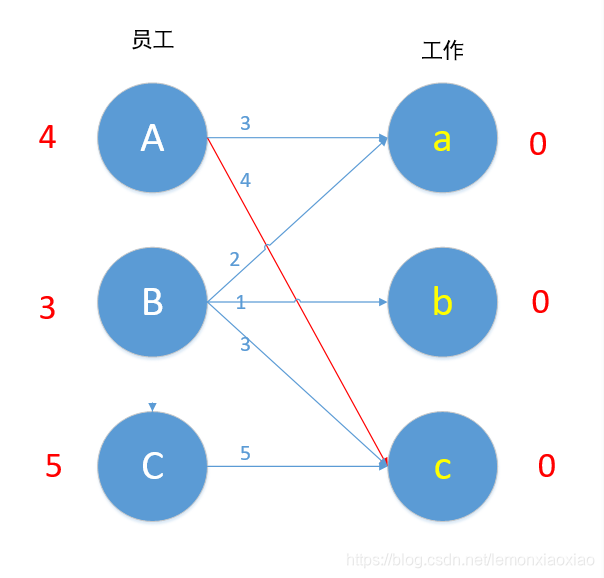
m2.png

接下来我们对B进行匹配，顶点B值为3，Bc边权重为3，匹配，但是A已经匹配c了，发生了冲突，怎么办？我们这时候第一时间应该想到的是，让B换个工作，但根据匹配原则，只有Bc边 3+0=3 满足要求，于是B不能换边了，那A能不能换边呢？对A来说，也是只有Ac边满足4+0=4的要求，于是A也不能换边，走投无路了，怎么办？

从常识的角度思考：其实我们寻找最优匹配的过程，也就是帮每个员工找到他们工作效率最高的工作，但是，有些工作会冲突，比如现在，B员工和A员工工作c的效率都是最高，这时我们应该让A或者B换一份工作，但是这时候换工作的话我们只能换到降低总体效率值的工作，也就是说，如果令R=左边顶点所有值相加，若发生了冲突，则最终工作效率一定小于R，但是，我们现在只要求最优匹配，所以，如果A换一份工作降低的工作效率比较少的话，我们是能接受的（对B同样如此）。

在KM算法中如何体现呢？

现在参与到这个冲突的顶点是A,B和c，令所有左边顶点值-1，右边顶点值+1，即 A-1,B-1，c+1，结果如下图所示。

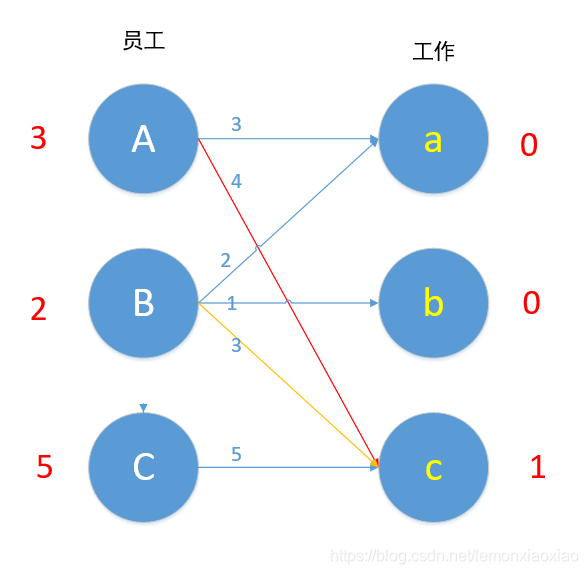
m3.png

我们进行了上述操作后会发现，若是左边有n个顶点参与运算，则右边就有n-1个顶点参与运算，整体效率值下降了1*（n-（n-1））=1 ，而对于A来说，Ac本来为可匹配的边，现在仍为可匹配边（3+1=4），对于B来说，Bc本来为可匹配的边，现在仍为可匹配的边（2+1=3），我们通过上述操作，为A增加了一条可匹配的边Aa，为B增加了一条可匹配的边Ba。

对B来说，Ba边 2+0=2，满足条件，所以B换边，a现在为未匹配状态，Ba匹配！

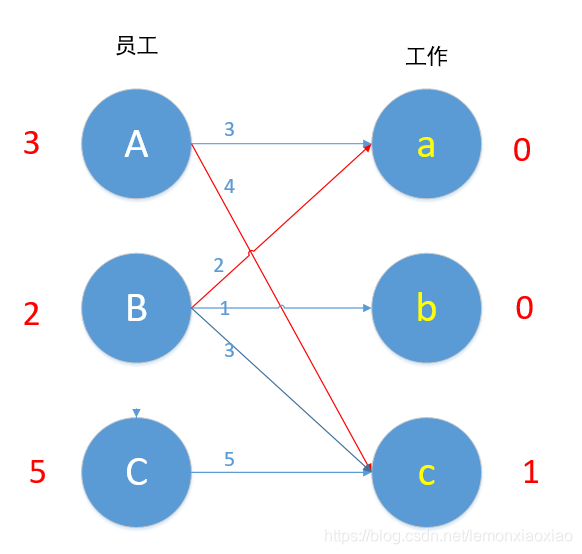
m4.png

我们现在匹配最后一条边C，Cc：5+1！=5，C边无边能匹配，所以直接C-1。（记住只有能匹配的情况下才使用匹配原则）

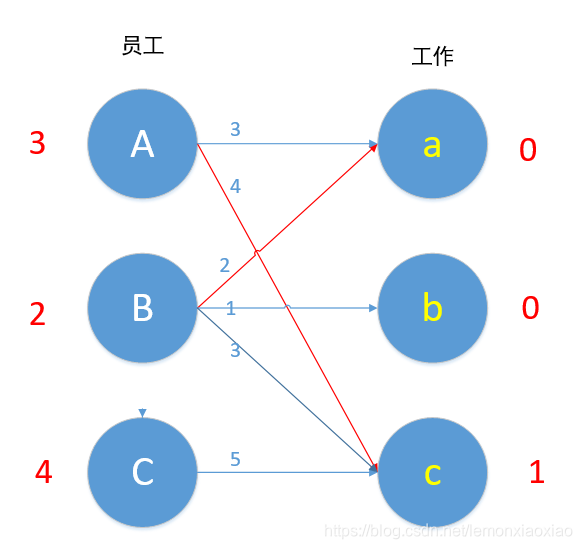
m5.png

现在Cc边 4+1=5，可以匹配，但是c已匹配了，发生冲突，C此时不能换边，于是便去找A，对于A来说，Aa此时也为可匹配边，但是a已匹配，A又去找B。

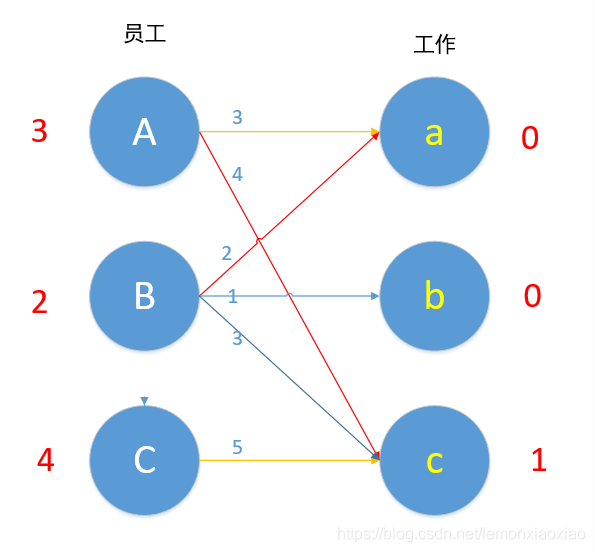
m6.png

黄色的线就是冲突的线，像交替路一样

B现在无边可以匹配了，2+0！=1 ，现在的路径是C→c→A→a→B，所以A-1，B-1，C-1，a+1，c+1。如下图所示。

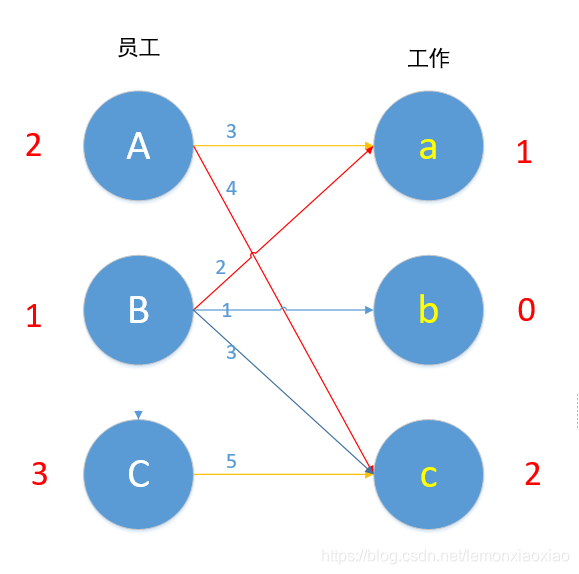
m7.png

对于B来说，现在Bb：1+0=1 可匹配！使用匈牙利算法，对此条路径上的边取反（匈牙利路径是Cc-cA-Aa-aB-Bb，其中aB和cA是已经匹配的，取反就剩下了，Cc/Aa/Bb 三组匹配，至此，两组匹配变成三组匹配，算法完成）。

m8.png

如图，便完成了此题的最优匹配。

这题中冲突一共发生了3次，所以我们一共降低了3次效率值，但是我们每次降低的效率值都是最少的，所以我们完成的仍然是最优匹配！

这就是KM算法的整个过程，整体思路就是：每次都帮一个顶点匹配最大权重边，利用匈牙利算法完成最大匹配，最终我们完成的就是最优匹配！

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
const int maxn = 300 + 10;
const int INF = 0x3f3f3f3f;

int wx[maxn], wy[maxn];//每个点的顶标值（需要根据二分图处理出来）
int cx[maxn], cy[maxn];//每个点所匹配的点
int visx[maxn], visy[maxn];//每个点是否加入增广路	
int cntx, cnty;//分别是X和Y的点数
int Map[maxn][maxn];//二分图边的权值
int slack[maxn];//边权和顶标最小的差值

bool dfs(int u)//进入DFS的都是X部的点
{
	visx[u] = 1;//标记进入增广路
	for (int v = 1; v <= cnty; v++)
	{
		if (!visy[v] && Map[u][v] != 0)//如果Y部的点还没进入增广路,并且存在路径
		{
			int t = wx[u] + wy[v] - Map[u][v];
			if (t == 0)//t为0说明是相等子图
			{
				visy[v] = 1;//加入增广路

				//如果Y部的点还未进行匹配
				//或者已经进行了匹配，可以从原来的匹配反向找到增广路
				//那就可以进行匹配
				if (cy[v] == -1 || dfs(cy[v]))
				{
					cx[u] = v;
					cy[v] = u;//进行匹配
					return 1;
				}
			}
			else if (t > 0)//此处t一定是大于0，因为顶标之和一定>=边权
			{
				slack[v] = min(slack[v], t);
				//slack[v]存的是Y部的点需要变成相等子图顶标值最小增加多少
			}
		}
	}
	return false;
}

int KM()
{
	memset(cx, -1, sizeof(cx));
	memset(cy, -1, sizeof(cy));
	memset(wx, 0, sizeof(wx));//wx的顶标为该点连接的边的最大权值
	memset(wy, 0, sizeof(wy));//wy的顶标为0
	for (int i = 1; i <= cntx; i++)//预处理出顶标值
	{
		for (int j = 1; j <= cnty; j++)
		{
			if (Map[i][j] == 0)continue;
			wx[i] = max(wx[i], Map[i][j]);
		}
	}
	for (int i = 1; i <= cntx; i++)//枚举X部的点
	{
		memset(slack, INF, sizeof(slack));
		while (1)
		{
			memset(visx, 0, sizeof(visx));
			memset(visy, 0, sizeof(visy));
			if (dfs(i))break;//已经匹配正确

			int minz = INF;
			for (int j = 1; j <= cnty; j++)
				if (!visy[j] && minz > slack[j])
					//找出还没经过的点中，需要变成相等子图的最小额外增加的顶标值
					minz = slack[j];
			//和全局变量不同的是，全局变量在每次while循环中都需要赋值成INF，每次求出的是所有点的最小值
			//而slack数组在每个while外面就初始化好，每次while循环slack数组的每个值都在用到
			//在一次增广路中求出的slack值会更准确，循环次数比全局变量更少


			//还未匹配，将X部的顶标减去minz，Y部的顶标加上minz
			for (int j = 1; j <= cntx; j++)
				if (visx[j])wx[j] -= minz;
			for (int j = 1; j <= cnty; j++)
				//修改顶标后，要把所有不在交错树中的Y顶点的slack值都减去minz
				if (visy[j])wy[j] += minz;
				else slack[j] -= minz;
		}
	}

	int ans = 0;//二分图最优匹配权值
	for (int i = 1; i <= cntx; i++)
		if (cx[i] != -1)ans += Map[i][cx[i]];
	return ans;
}
int n, k;
int main()
{
	while (scanf("%d", &n) != EOF)
	{
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
				scanf("%d", &Map[i][j]);
		}
		cntx = cnty = n;
		printf("%d\n", KM());
	}
	return 0;
}

更多深入

  1. 算法学习笔记(5)：匈牙利算法及题目
  2. 带你入门多目标跟踪（三）匈牙利算法&KM算法